In this page, you will learn how to enter your preference parameters:

• Preference Functions
• Preference Thresholds
• Preference Threshold
• Indifference Threshold
• Minimize/Maximize
• Absolute/Relatif
• Enter a Scale (for qualitative data)
• How to modify the weigths.
• Flow Viewer for a criterion

---

Preference parameters:

Access:

To have access to the preference parameters:

• Menu: Problem --> Parameters of the criteria (see Fig.1), or
• Choose the Tab "Parameters" in the Frame Data (see Fig.2)

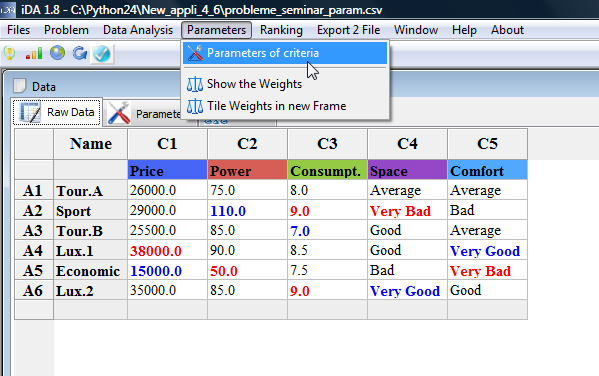Fig.1.

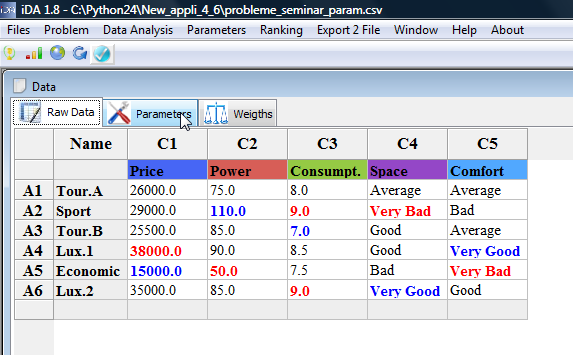Fig.2

and you will come to the following frame:

Fig.3

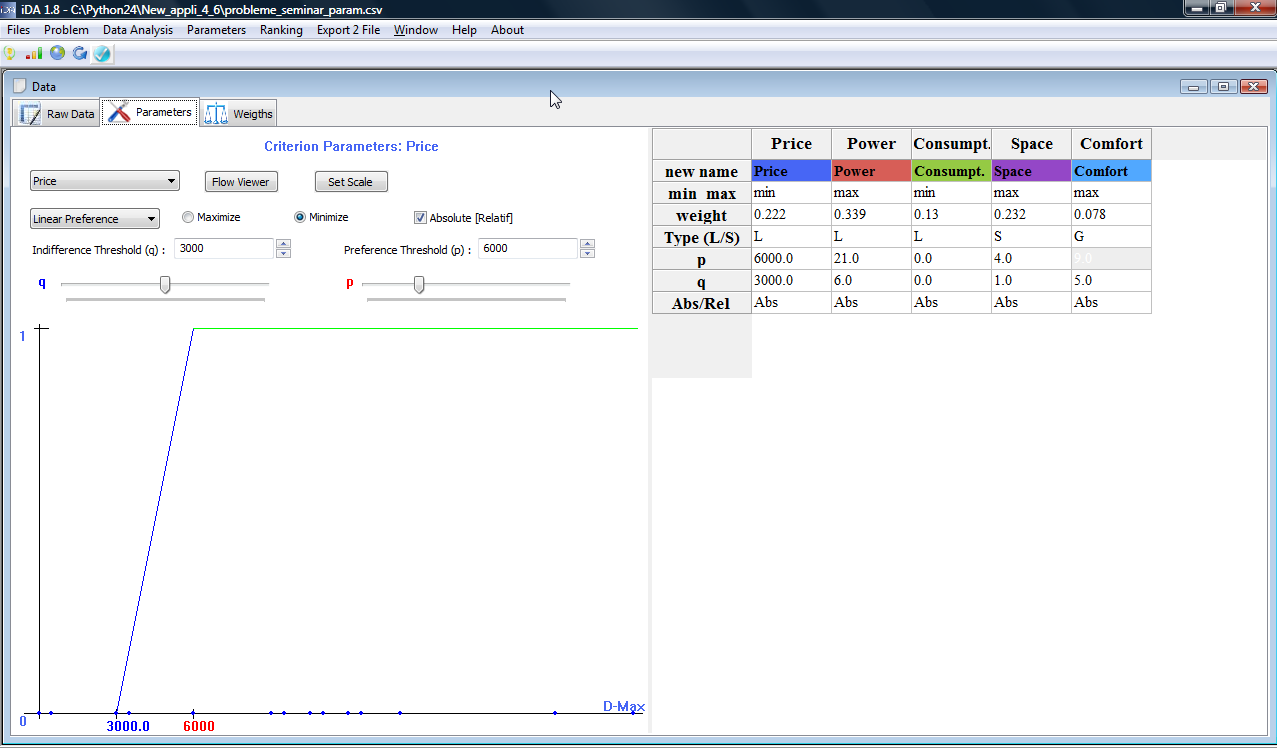
Legend: Here are the different preference parameters :


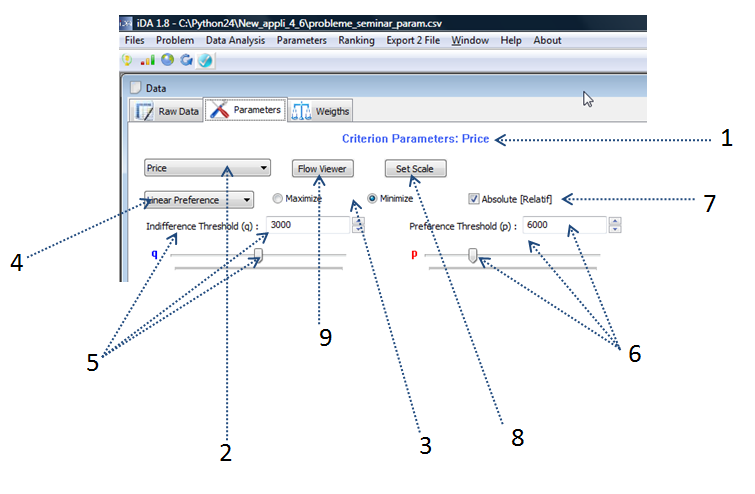
Fig.4.

With following associations:

1. Gives you the name of the current criterion that you modify (here: Criterion 1: Price)
2. You can change the criterion for which you want to modify the parameters. (here: Price)
3. Min/max: You can precise if you want to maximize or minimize your criterion (here: Minimize)
4. Preference Function: You can choose your preference function: either linear function, step wise or gaussian function.
5. Indifference threshold: here can enter directly a specific value for the indifference threshold or change the value by changing the cursor on the slider.
6. Preference threshold: here can enter directly a specific value for the preference threshodl or change the value by changing the cursor on the slider.
7. Absolute/Relatif: You can choose to compare the absolute values or the the relative values (and thus woriking in percentages)
8. Set Scale: You can enter a specific scale for qualitative criteria (eg., the confort)
9. Flow Viewer: here you can directly see the scores for the considered criterion of the different actions as well as the distributions, etc.

---

Min-Max:
Specifiy if you want to maximize or minimize your criteria. Generally, the price of a car has to be minimized for a buyer whereas the power of a car has to be maximized.





Prefence Function and Preference Thresholds:
The prefrence function will translate your preference when comparing two actions on one criterion. It expresses the way you feel the difference between the performances of the actions. The insensity of the preference (on the axis left) is in function of the difference between the evaluations of the actions.

---

There are two main thresholds:

• the preference threshold (P): as soon as the difference between the evaluations is higher than this threshold, the preference will be 1. You will thus definitely prefer one of the two actions of the other.
• the indifference threshold (Q): as long as the difference between the evaluations is lower than this threshold, the preference is 0. There will be no difference between the two actions.

If the difference is between these two thresholds, there will be an interpolation computed which depends on the prefence function.

For instance, consider two cars which prices are 10000€ and 13000€. Suppose you want to minimize the price. How is the car of 10000€ preferred to the car of 13000€ ? This will be given by the preference functions which may be linear, step-wise or gaussian.

1. Linear Preference Function:
• With indifference and preference threshold equal to zero (p=q=0): this means thus that you strongly prefer the car of 10000€. The preference is 1. (see Fig.5)
• With indifference threshold = 0 and preference threshold = 5000: this means thus that you prefer the car of 10000€ with a preference degree equal to (13000-10000)/5000=3000/5000=0.6 (See Fig.6)
• With indifference threshold = 2000 and preference threshold = 5000:  this means thus that you prefer the car of 10000€ with a preference degree equal to (13000-10000 - 2000)/(5000)=1000/5000=0.2. The indifference threshold is thus the difference (in price) for which you feel no preference (if you choose q=2000€, you consider that two cars are equal if their difference in price is smaller than 2000€). (See Fig.7)


2. The Step Wise Function
• If the difference between the two cars are smaller than q --> no preference ; if  q < difference < p: preference=0.5 ; if difference >p: preference=1. For instance if q=2000 and p=5000, the car of 10000€ will be preferred to the car of 13000€ with a preference of 0.5 (See Fig.8).


3. The Gaussian Function
• This function is usually used when small differences induce small preferences, whereas high differences, high preferences. You can the point when the preferences will significantly increase: this is given by the inflexion point (s).  (See Fig.9)

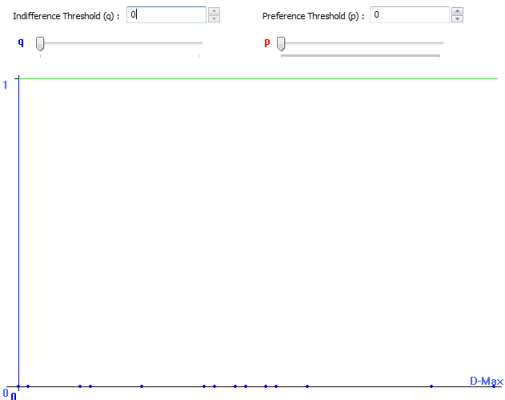Fig. 5: Q=0=P

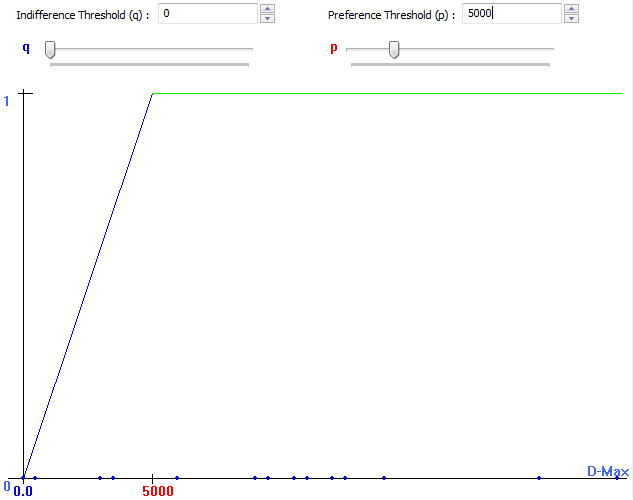Fig. 6. Linear: Q=0 ; P=5000

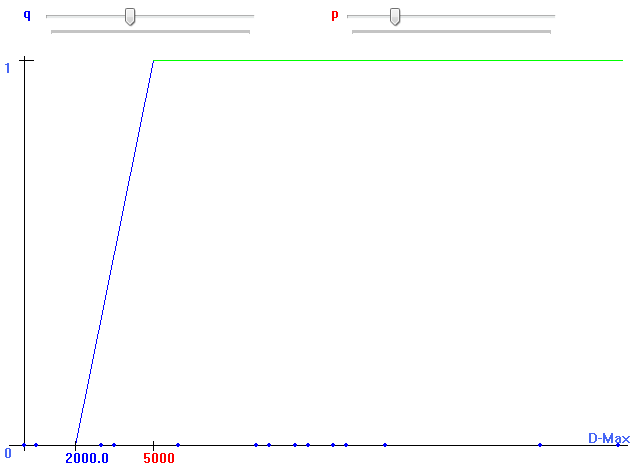Fig.7.Linear: Q=3000 ; P=5000

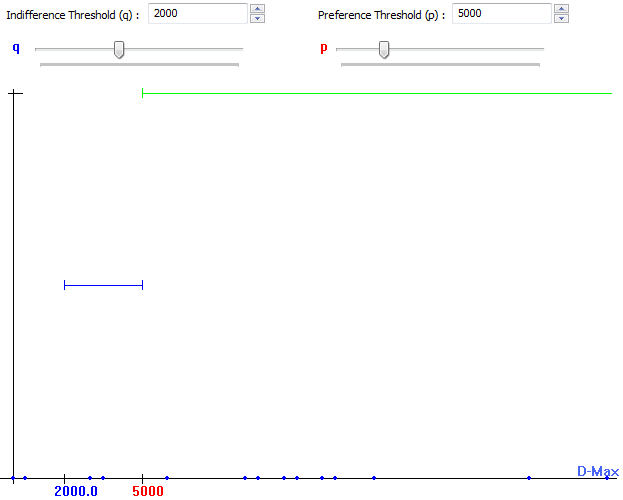Fig.8. Step: Q=2000, P=5000

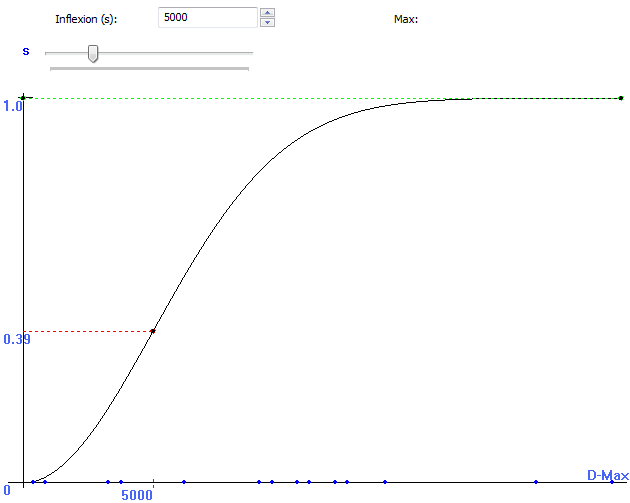Fig.9.: Gaussian: S=5000

---

Absolute/Relatif
When comparing the evaluations of the actions, you can either think in terms of absolute values (eg;, 1000 and 2000 will lead to a difference of 1000) or relatively (eg;, 1000 and 2000 will lead to a difference of 100%). The thresholds will be compared to difference, either their absolute diffrence or either their relative difference.

---

Scale
Choose a scale for your qualitative data. For instance, the confort of a car, can lead to bad, good, very good. In order to compare them, you have to enter a scale.

Click on Propose Scale (Top-Left in the Set a scale Frame) to get all the different possible scale values, order them by means of Up and Down (Top-Left in the Set a scale Frame) and enter your values for the different scales.
Don't forget to save your scale (Save Scale) , otherwise it will not have an effect. You can check if your scales have been saved, by looking at your Preprocessed Data.

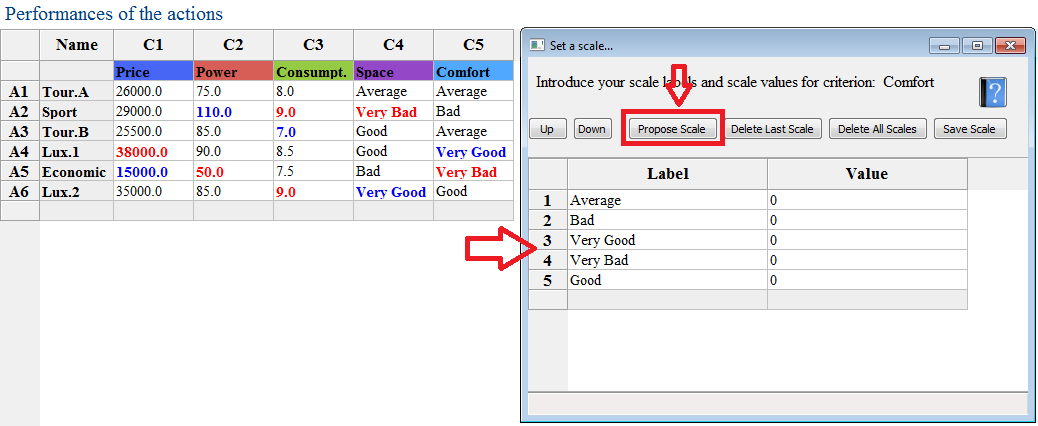
1. Click on the button Set Scale (number 8 in Fig.4 at the top of this page ).





2. Click on 'Propose scale' ; this will give you all the different terms/lables present in the date for the considerd comfort. In thsi case, we have thus: Average, Bad, Very Good, Very Bad and Good.




3. Order the labels from the best to the worst.
 



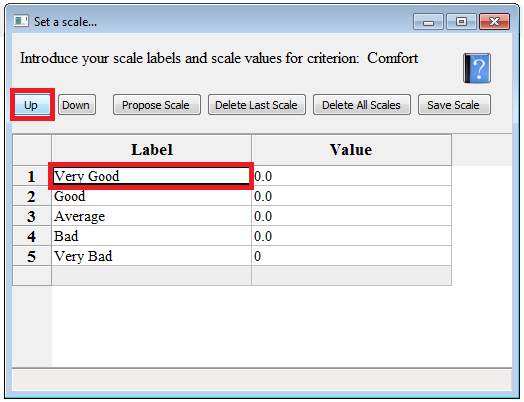
4. Introduce the values your consider for each value and Save the scale.



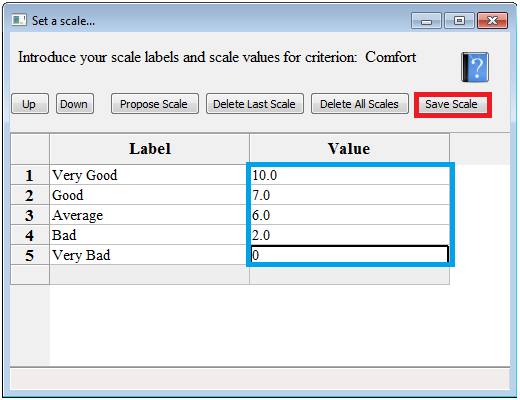
To delete a scale, click on 'Delete All Scales' and Save it ! Your criterion will be considered then as having numerical values; in other words: you will treat your data as usual.

---

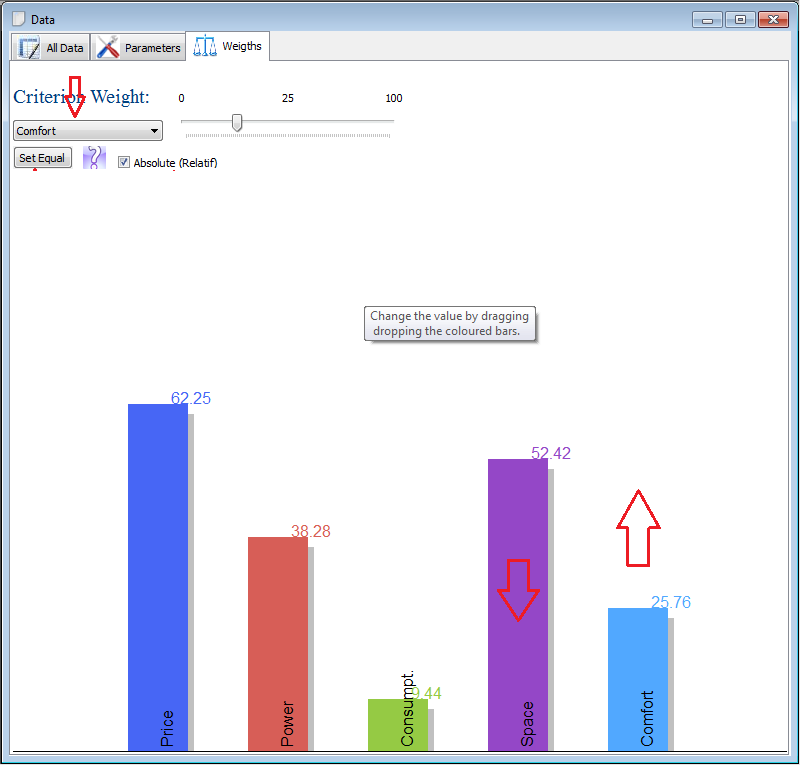
Weights

You need to define the relative importance of each criterion. This is an essential step in the introduction of your preferences. A weight of criterion is relative importance compared to the other criteria.
In a problem with two criteria, if criterion A has a weight 2 and criterion B, this means that the criterion A is considered as twice as important as criterion B.

There are different ways to define the weights:

1. choose the criterion in the list-box ; and use the slider-box to define its value. You will see the height of the weights changing.
2. While clicking left on a weight bar, move the mouse up and down to change the value (i.e. drag your mouse).
3. Click on the Question mark to go the Weight wizard ; this will help you to define the weights if you have no idea about their values.
4. Click on Set equal if all weights have the same importance.

By ticking the box Absolute (Relatif) the value of all the weights will change relatively or just the value of one criterion.




To get some help for defining your weights more accurately, click on the Question logo

This will lead to the following frame: Help Weight Wizard Frame

---

Flow Viewer